Posted in O NAMA, ДРУЖЕЊЕ, МАТЕМАТИКА

Скуп

   7 маја, 2016
За другу употребу, погледајте страницу Скуп (структура података).

У математици, скуп је појам који се обично не дефинише, већ се узима као основни, а често се умјесто тог термина користе разни синоними, као што су, на примјер, мноштво, фамилија, колекција исл.

За означавање скупова се најчешће користе велика слова латинице A, B, \ldots\,. Ако је неки скуп коначан или пребројиво бесконачан, па се његови елементи могу набројати, користи се запис

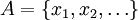A = \{x_{1}, x_{2}, \ldots, x_{n}\}\,, односно A = \{x_{1}, x_{2}, \ldots\}\,;

такође, елементи неког скупа се могу описати коришћењем неког својства 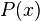P(x)\, које они (и само они) задовољавају:

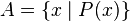
A = \{x \mid P(x)\}\,

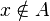Дакле, скуп је одређен својим елементима; припадност елемента x\, скупу A\, означава се са x \in A, а неприпадност са x \notin A.

Између скупова се уводе две основне релације – једнакост и инклузија:

A = B \Leftrightarrow (\forall x)(x \in A \Leftrightarrow x \in B)

A \subset B \Leftrightarrow (\forall x)(x \in A \Rightarrow x \in B)

Непосредно из ових дефиниција је јасно да је

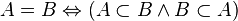
A = B \Leftrightarrow (A \subset B \land B \subset A)

Празни скуп, који се означава са \O може се дефинисати, на пример, помоћу \O = \{x \mid x \neq x\}. Тај скуп има особину да је \O \in A за било који скуп A. Такође, ако су у оквиру неке теорије сви скупови са којима се оперише подскупови неког фиксираног скупа, тај скуп се назива универзалним и често обиљежава са U. Такав скуп има особину да је A \in U за све скупове A са којима се оперише у датом проблему, при чему треба нагласити да није исправно користити термин „скуп свих скупова“ – он може довести до нежељених парадокса.

Савремена теорија скупова настаје крајем 19. века када немачки математичар Георг Кантор даје описну математичку теорију која се још назива и интуитивна или наивна теорија скупова.

Дефиниција
Скуп је обједињење извесних елемената у једну целину.

Овде ће бити представљен систем аксиома каквог га је поставио Готлоб Фреге у књизи „Основни закони аритметике“ 1893. године

Аксиома о једнакости два скупа
Два скупа су једнака ако и само ако имају исте елементе.
Аксиома апстракције
За унапред задато својство P(x) постоји скуп {x|P(x)} чији су елементи управо они објекти који имају то својство.
Аксиома избора
За сваки непразан скуп S постоји функција f чији су оригинали непразни подскупови тог скупа, а слике су елементи оригинала, тј.

(\forall S)(\exist f:P(S)\ {\emptyset}\longrightarrow S)(\forall A)(A\subset S \land A \ne \emptyset \Longrightarrow f(A) \in A)

Последња аксиома каже да свако својство дефинише скуп. Међутим, већ 1902. године ће Бертранд Расел показати пример који води контрадикцији. То добија назив Раселов парадокс, а теорија скупова се нашла пред великим проблемима.

Са скуповима се могу изводити разне операције. Следе дефиниције неколико основних:

A \cup B = \{x \mid x \in A \lor x \in B\}

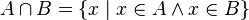
A \cap B = \{x \mid x \in A \land x \in B\}

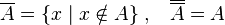
\overline{A} = \{x \mid x \notin A \} \;,\;\;\;\overline{\overline{A}} = A

A \setminus B = \{x \mid x \in A \lor x \notin B\} = A \cap \overline{B}

A \vartriangle B = \{ x \mid x \in A \cup B \land x \notin A \cap B \} = (A \cup B) \cap (\overline{A} \cup \overline{B})

Основне особине скупова су задате у следећој листи:

A \cup B = B \cup A, A \cap B = B \cap A (закони комутације)

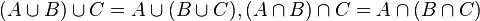(A \cup B) \cup C = A \cup (B \cup C), (A \cap B) \cap C = A \cap (B \cap C) (закони асоцијације)

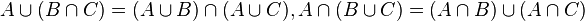A \cup (B \cap C) = (A \cup B) \cap (A \cup C), A \cap (B \cup C) = (A \cap B) \cup (A \cap C) (закони дистрибуције)

\overline{A \cup B} = \overline{A} \cap \overline{B}, \;\; \overline{A \cap B} = \overline{A} \cup \overline{B}

За радознале:

Author: УЧИТЕЉ ДЕЈАН