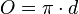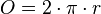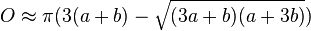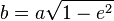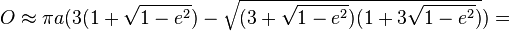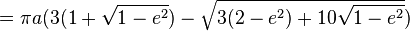Posted in O NAMA, ДРУЖЕЊЕ, МАТЕМАТИКА, ЧАСОВИ

Обим

   1 априла, 2016

Обим представља дужина затворене линје. Уколико ова линија ограничава неки геометријски објекат, онда је њен обим и обим тог тела. По правилу, обим се обележава великим латиничним словом O.

Обим круга се може израчунати помоћу његовог пречника коришћењем формуле:

O = \pi \cdot d \,

Или, замјеном пречника полупречником:

O = 2 \cdot \pi \cdot r \,

где је r полупречник (радијус), а d пречник круга, и π (грчко слово пи) је константа приближно једнака 3,1415926.

Дакле, однос обима и пречника круга је π.

Обим елипсе се рачуна коришћењем коначних редова. Добру апроксимацију је дао индијски математичар Шринваса Рамануџан:

O \approx \pi (3(a+b) - \sqrt{(3a+b)(a+3b)})

где су a и b полуосе осовине. На основу њих се може израчунати ексцентрицитет елипсе:

b = a \sqrt{1-e^2}

Што значи да обим може приближно бити изражен као:

O \approx \pi a (3(1+\sqrt{1-e^2}) - \sqrt{(3+ \sqrt{1-e^2})(1+3 \sqrt{1-e^2})}) =
= \pi a (3(1+\sqrt{1-e^2}) - \sqrt{3(2-e^2)+10 \sqrt{1-e^2}})

 

Објавио:

Немања Вучковић

Author: УЧИТЕЉ ДЕЈАН